Producto Escalar

El estudio de vectores y matrices es la médula del álgebra lineal. El estudio de vectores comenzó esencialmente con el trabajo del gran matemático irlandés sir William Hamilton. Su deseo de encontrar una forma de representar un cierto tipo de objetos en el plano y el espacio lo llevó a descubrir lo que él llamó cuaterniones. Esta noción condujo al desarrollo de lo que ahora se conoce como vectores. (R2)

Sir William Hamilton

Muchas cantidades mensurables, como la longitud, el área, el volumen, la masa y la temperatura, pueden describirse completamente al especificar su magnitud. Otras cantidades, como la velocidad, la fuerza y la aceleración, requieren tanto una magnitud como una dirección para su descripción. Estas cantidades son vectores. Por ejemplo, la velocidad del viento es un vector que consta de rapidez del viento y su dirección, como 10 km/h suroeste. Geométricamente, los vectores se representan con frecuencia como flechas o segmentos de recta dirigidos. (R3)

Vector Fila

Un vector de n componentes se define como un conjunto ordenado de n números escritos de la siguiente manera:

$\left ( x_{1},x_{2},...,x_{n} \right )$

Vector Columna

Un vector columna de n componentes es un conjunto ordenado de n números escritos de la siguiente manera:

$\begin{pmatrix} x_{1}\\ x_{2}\\ ...\\ x_{n} \end{pmatrix}$

Donde están los vectores?

Los vectores surgen de diversas maneras. Suponga que el jefe de compras de una fábrica debe ordenar cantidades diferentes de acero, aluminio, aceite y papel. Él puede mantener el control de las unidades a ordenar con un solo vector donde a cada posición se le asocia algún tipo de material, si pensamos en asociar en la primera posición la cantidad de acero, en la segunda posición la cantidad de aluminio, en la tercera posición la cantidad de aceite y en la cuarta posición la cantidad de papel. Entonces el vector

$\begin{pmatrix} 10\\ 30\\ 15\\ 60 \end{pmatrix}$

indica que ordenará 10 unidades de acero, 30 unidades de aluminio, etcétera.

Creando un vector en Scilab.

Para definir un vector simplemente colocamos los valores entre corchetes[] y separamos los valores con espacios o comas(,) y le damos un nombre a la variable. Para crear un vector columna debemos separar los valores entre(;).

EJEMPLO 1:

Crear el vector Fila v=(2,3,4-3i)

v=[2,3,4-3i]

EJEMPLO 2:

Crear el vector filas

u=(-1,3,8,11) y el vector columna

$u=\begin{pmatrix} 2\\ 3\\ 4\\ -3i \end{pmatrix}$

Respuesta:

u=[-1,3,8,1]

v=[2;3;4;-3*%i]

Resultado en Scilab:

Producto Escalar de Vectores:

Sean
$a=\left ( a_{1},a_{2},...,a_{n} \right )$ y
$b=\begin{pmatrix} b_{1}\\ b_{2}\\ .\\ .\\ .\\ b_{n} \end{pmatrix}$ .

Entonces el producto escalar de a y b denotado a·b, esta dado por

$a\cdot b=a_{1}b_{1}+a_{2}b_{2}+...+a_{n}b_{n}$ (3)

Debido a la notación en (3), el producto escalar se llama con frecuencia producto punto o producto interno de los vectores. Observe que el producto escalar de dos vectores de dimensiones n es un escalar (es, decir es un número).

El producto vectorial debe ser entre un vector fila y un vector columna.

EJEMPLO 2:

Sea

$a=(2,-5,4,-6)$

$b=\begin{pmatrix} 1\\ 0\\ -7\\ 3 \end{pmatrix}$

Calcule a·b

Respuesta:

$a\cdot b = (2)(1)+(-5)(0)+ (4)(-7)+ (-6)(3) = 2 +0+(-28)-18 =-44$

En Scilab:

Paso 1: Abrir Scinotes

Abriendo Scinotes

El símbolo (*) se utiliza para el producto escalar. Vamos a ejecutar nuestro código en SciNotes para ello nos vamos al menú aplications->Scinotes. Y allí escribimos lo siguiente:

u=[2,-5,4,-6]; //Vector Fila

v=[1;0;-7;3]; //Vector Columna

uxv= u*v;

disp(uxv);

Descargar

Paso 2: Guardar y Ejecutar

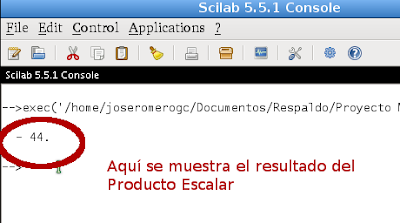
Hacemos clic en el botón de Guardar y Ejecutar para que nos muestre el resultado:

Ejemplo Práctico 1: Joyería

Un fabricante de joyería de diseño tiene órdenes por dos anillos, tres pares de aretes, cinco prendedores y un collar. El fabricante estima que le llevará 1 hora de mano de obra hacer un anillo, 1½ horas hacer un par de aretes, ½ hora para un prendedor y 2 horas para un collar.

a)Exprese las órdenes del fabricante como un vector Fila.

b)Exprese los requerimientos en horas para los distintos tipos de joyas como un vector columna.

c)Utilice el producto escalar para calcular el número total de horas que requerirá para terminar las órdenes.

RESPUESTA:

a) Se necesitan 2 anillos, 3 pares de aretes y 5 prendedores

Vector Ordenes:

Ordenes = [2,3,5];

a) Se necesitan 1 hora para la mano de obra ,½ para el anillo anillos y 2 para el collar

Vector Tiempo:

Tiempo = [1;1/2;2];

c) TotalHoras = Ordenes*Tiempo;

Este es el código en Scilab:

Ordenes = [2,3,5]; //Vector Ordenes

Tiempo = [1;1/2;2]; //Vector Tiempo

TotalHoras = OrdenesTiempo; //Total de Horas*

disp(TotalHoras)

Lo cual da como resultado 13,5 horas para poder terminar los pedidos

Descarga:

Acerca del Autor Matemática Positiva

Sitio Web Dedicado al Universo Matemático

.

Archivo del blog

Datos personales

Producto Escalar

Respuesta:

u=[-1,3,8,1]